728x90
반응형

728x90
반응형
🙆♂️ 그래프
그래프란 노드와 그 노드를 모아놓은 간선을 하나로 모은 자료구조
하나의 객체와 다른 객체가 연결되어 있는 구조
종류
무방향 그래프 > 간선에 방향이 없음
방향 그래프 > 간선에 방향이 있음
가중치 그래프 > 간선에 가중치가 할당된 그래프, 네트워크라고도 부른다.
부분 그래프 > 특정 그래프에서 일부분을 때어낸 그래프
용어
노드, 간선, 인접 정점
차수 > 연결되어 있는 간선 수
무방향 그래프 : 차수의 합 == 간선 * 2
방향 그래프 : 진입차수와 진출차수가 존재함. 모든 진입차수의 합은 간선의 수
단순경로 - 경로 중 반복되는 간선이 없는 경로
사이클 - 시작 정점과 종료 정점이 동일한 경로
연결 그래프 - 모든 정점들 사이에 경로가 존재하는그래프
트리 - 사이클을 가지지 않는 연결 그래프, 실제로 루트를 정하면 트리모양으로 만들 수 있음
완전 그래프 - 모든 정점 간에 간선이 존재할 때
구현
인접 행렬 or 인접 리스트 or 노드와 같이 리스트로
제일 좋은 것은 딕셔너리와 set을 활용하여 구현
"""
A - C - E - G
| | |
B - D - F H
"""
graph = {
'A':set(['B','C']),
'B':set(['A','D']),
'C':set(['A','D','E']),
'D':set(['B','C','F']),
'E':set(['C','G','H']),
'F':set(['D']),
'G':set(['E','H']),
'H':set(['G']),
}
graph['C']
탐색
DFS ( 깊이 우선 탐색)
def dfs(graph,start,visited=set()):
if start not in visited:
visited.add(start)
print(start, end=' => ')
subt = graph[start] - visited
for v in subt:
dfs(graph,v,visited)
"""
A - C - E - G
| | |
B - D - F H
"""
dfs(graph,'A')
BFS ( 너비 우선 탐색 )
import collections
def bfs(graph,start):
visited = set([start])
queue = collections.deque([start])
while queue:
vertex = queue.popleft()
print(vertex, end=" => ")
subt = graph[vertex] - visited
for v in subt:
visited.add(v)
queue.append(v)
"""
A - C - E - G
| | |
B - D - F H
"""
bfs(graph,'A')
연결 성분
최대로 연결된 부분 그래프들을 구함
"""
C - A - B > graph
D - E > graph
"""
graph = {
'A':set({'B','C'}),
'B':set({'A'}),
'C':set({'A'}),
'D':set({'E'}),
'E':set({'D'}),
}
def find_com(graph):
allvisited = set()
g_com = []
for v in graph:
if v not in allvisited:
visited = set()
dfs(graph,v,visited)
allvisited.update(visited)
g_com.append(visited.copy())
print(visited)
find_com(graph)
신장 트리
그래프 내의 모든 정점을 포함하는 트리
사이클 x
graph = {
'A':set(['B','C']),
'B':set(['A','D']),
'C':set(['A','D','E']),
'D':set(['B','C','F']),
'E':set(['C','G','H']),
'F':set(['D']),
'G':set(['E','H']),
'H':set(['G']),
}
import collections
def bfs(graph,start):
visited = set([start])
queue = collections.deque([start])
while queue:
vertex = queue.popleft()
# print(vertex, end=" => ") bfs에서 이건 지워지고
subt = graph[vertex] - visited
for v in subt:
print(f"({vertex}, {v})", end=" => ")
visited.add(v)
queue.append(v)
"""
A - C - E - G
| | |
B - D - F H
"""
bfs(graph,'A')
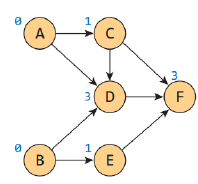
위상정렬
방향 그래프에 대한 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것
728x90
반응형
'코딩테스트 > 알고리즘&자료구조' 카테고리의 다른 글
| [자료구조] 트리 - 탐색 트리 (0) | 2022.12.20 |
|---|---|
| [자료구조] 트리 - 일반 트리, 이진 트리, 결정트리, 힙 (0) | 2022.12.20 |
| [자료구조][파이썬으로 쉽게 풀어쓴 자료구조] 05 큐 문제풀기 (0) | 2022.10.25 |
| [자료구조] 큐 - 우선순위 큐를 활용한 미로 탐색 (0) | 2022.10.25 |
| [자료구조] 큐 - BFS 미로 탐색 (0) | 2022.10.25 |