🙆♂️일반 트리
트리 : 계층적인 자료의 표현에 적합한 자료 구조다.
최상위 노드를 루트 노드라 부름.
자식을 갖지 못하는 노드 = 단말 노드
class TNode:
def __init__(self,data, left, right):
self.data = data
self.left = left
self.right = right
d = TNode('D',None,None)
e = TNode('E',None,None)
f = TNode('F',None,None)
b = TNode('B',d,e)
c = TNode('C',f,None)
a = TNode('A',b,c)
🙆♂️이진 트리
이진 트리 : 모든 노드가 2개의 서브 트리를 갖는 트리

완전 이진트리 : 왼쪽부터 꽉찬 경우
포화 이진트리 : 모든 노드가 꽉차있는 경우
이진트리의 특징1 : 노드의 개수가 n개면 간선의 개수는 n-1이다.
이진트리의 특징2 : 높이가 h이면 h~2^h-1개의 노드를 가짐.
> 반대로 생각하면 n개 노드의 이진 트리 높이는 log2(n+1) ~ n이다.
표현법
1.배열 표현법
2. 연결된 구조
배열 표현법
장점 - 구현이 쉬움
단점 - 메모리 낭비가 심함.
연결된 구조

공간의 제약이 적습니다.
순회
순회란 트리에 속하는 모든 노드를 한 번씩 방문하는 것입니다.
1. 전위 순회
2. 중위 순회
3. 후위 순회
4. 레벨 순회
전위 순회 : 루트 > 왼쪽 서브트리 > 오른쪽 서브트리
특징 - 부모를 처리한 다음에 자식을 처리하는 경우
class TNode:
def __init__(self,data, left, right):
self.data = data
self.left = left
self.right = right
def pre(n):
if n is not None:
print(n.data, end=" ")
pre(n.left)
pre(n.right)
# A
# B C
#DE F
d = TNode('D',None,None)
e = TNode('E',None,None)
f = TNode('F',None,None)
b = TNode('B',d,e)
c = TNode('C',f,None)
a = TNode('A',b,c)
pre(a)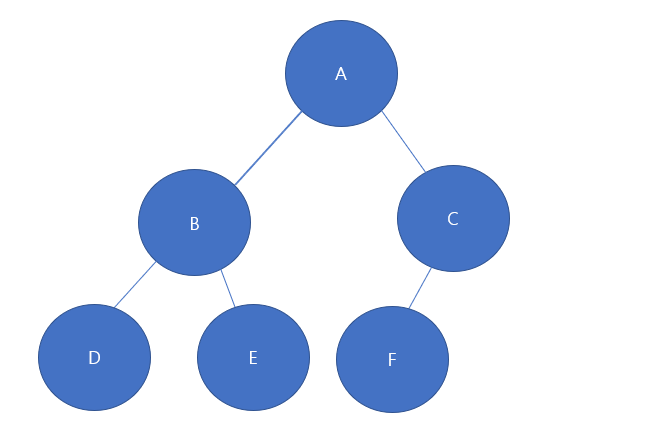
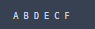
중위 순회 : 왼쪽 서브트리 > 루트 > 오른쪽 서브트리
특징 - 이진탐색트리의 경우 제일 작은 값이 왼쪽 아래에 위치하게 되어서 정렬에 용이합니다.
def inO(n):
if n is not None:
inO(n.left)
print(n.data, end=" ")
inO(n.right)
inO(a)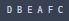
후위 순회 : 왼쪽 서브트리 > 오른쪽 서브트리 > 루트
def post(n):
if n is not None:
post(n.left)
post(n.right)
print(n.data, end=" ")
post(a)
레벨 순회 : 노드를 레벨 순으로 검사하는 순회 방법
큐를 이용해서 구현할 수 있음.
from queue import Queue
def level(root):
queue = Queue()
queue.put(root)
while not queue.empty():
n = queue.get()
if n is not None:
print(n.data, end=" ")
queue.put(n.left)
queue.put(n.right)
level(a)
연산
노드 개수 : 아래에서 위로 각 자식의 후손 노드 수를 합해서 올라가서 최종적으로 루트 노드에서 총 합을 구하게 되는 방식입니다.
def cntN(n):
if n is None:
return 0
else:
return cntN(n.left) + cntN(n.right)+1
cntN(a)
단말 노드의 수 : 단말 노드인 경우만 sum
def cntL(n):
if n is None:
return 0
elif n.left ==None and n.right ==None:
return 1
else:
return cntL(n.left) + cntL(n.right)
cntL(a)
트리의 높이 : 좌우 서브 트리 중 더 큰 서브트리에 1을 더해서 높이 구함.
def tree_H(n):
if n is None:
return 0
return max([tree_H(n.left),tree_H(n.right)])+1
tree_H(a)
🙆♂️ 결정 트리
여러 단계의 복잡한 조건을 갖는 문제에 대해 조건과 그에 따른 해결 방법을 트리 형태로 나타낸 것.
모스부호를 통한 실습 :
모스 부호 테이블
table = [('A', '.-'), ('B', '-...'),
('C', '-.-.'), ('D', '-..'), ('E', '.'),
('F', '..-.'), ('G', '--.'), ('H', '....'),
('I', '..'), ('J', '.---'), ('K', '-.-'),
('L', '.-..'), ('M', '--'), ('N', '-.'),
('O', '---'), ('P', '.--.'), ('Q', '--.-'),
('R', '.-.'), ('S', '...'), ('T', '-'),
('U', '..-'), ('V', '...-'), ('W', '.--'),
('X', '-..-'), ('Y', '-.--'), ('Z', '--..')]
결정 트리 생성
def d_tree():
root = TNode(None,None,None)
for mrs in table:
code = mrs[1]
node = root
for c in code:
if c == ".":
if node.left == None:
node.left = TNode(None,None,None)
node = node.left
elif c == "-":
if node.right == None:
node.right = TNode(None,None,None)
node = node.right
node.data = mrs[0]
return root
mrsTree = d_tree()
문자열 > 모스부호 인코딩
def enc(text):
code_lst = []
for c in text:
idx = ord(c) - ord('A')
code = table[idx][1]
code_lst.append(code)
return code_lst
python_code = enc("PYTHON")
print(python_code)
모스부호 > 문자열 디코딩
def decode(mrsTree, code_lst):
text = ""
for code in code_lst:
node = mrsTree
for c in code:
if c == '.':
node = node.left
elif c == "-":
node = node.right
text = text+node.data
return text
print(decode(mrsTree,python_code))
🙆♂️ 힙
힙은 완전이진트리 기반의 자료구조, 최대값 혹은 최소값을 root에 올리고 이를 바탕으로 빠르게 값을 찾는 트리입니다.
1. 최대 힙
2. 최소 힙
3. 힙이 아님
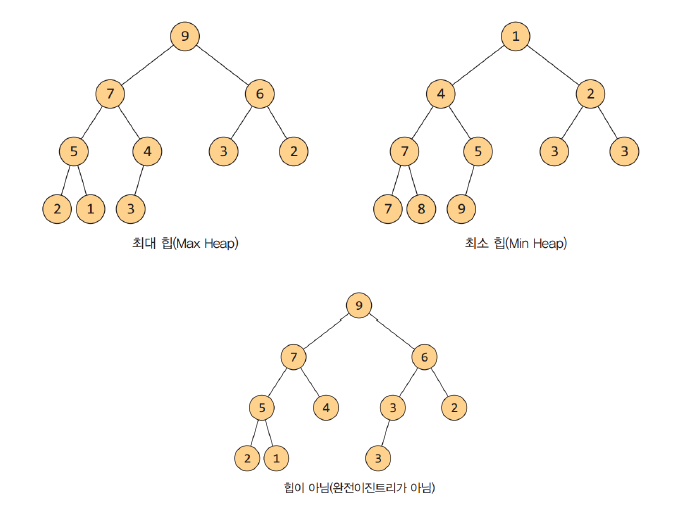
최대힙
class MaxHeap:
def __init__(self):
self.heap=[]
self.heap.append(0)
def size(self): return len(self.heap) -1
def isEpt(self): return self.size() == 0
def Parent(self, i):
return self.heap[i//2]
def Left(self, i):
return self.heap[i*2]
def Right(self, i):
return self.heap[i*2+1]
def display(self):
print("heap : ",self.heap[1:])
연산
1. 삽입연산
삽입연산은 힙이여서 가능한거임 즉 완전이진트리라 가능
삽입한 노드와 루트 노드 크기 비교해서 삽입한 노드가 크다면 루트노드와 교환
def insert(self,n):
self.heap.append(n)
i = self.size()
while (i != 1 and n > self.Parent(i)):
self.heap[i]=self.Parent(i)
i=i//2
self.heap[i]=n
heap = MaxHeap()
heap.insert(2)
heap.display()
heap.insert(5)
heap.display()
heap.insert(4)
heap.display()
heap.insert(8)
heap.display()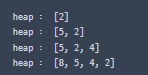
2. 삭제 연산
def delete(self):
if not self.isEmt():
hroot = self.heap[1] #삭제할 값
last = self.heap[self.size()] #힙의 제일 마지막 값이 최상단으로
self.heap.pop(-1) #삭제함
i=1
while(i*2<=self.size()):
max_idx = 0 #좌
if i*2+1 < self.size() and self.Left(i) < self.Right(i):
max_idx=1 #우
if last >= self.heap[i*2 + max_idx]: #최상단으로 간 마지막값과 자식 중 큰 값이랑 비교
break #last가 크져서 더 이상 노드를 변경하지 않아도 되는 경우 탈출
self.heap[i] = self.heap[i*2+max_idx] #last가 있던 값과 교환당하는 코드
i = i*2 + max_idx # i 값에 더큰 자식 노드 저장
self.heap[i] = last
return hroot
heap = MaxHeap()
heap.insert(2)
heap.display()
heap.insert(5)
heap.display()
heap.insert(4)
heap.display()
heap.insert(8)
heap.display()
print(heap.delete())
heap.display()
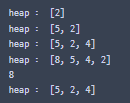
'코딩테스트 > 알고리즘&자료구조' 카테고리의 다른 글
| 그래프 (0) | 2022.12.20 |
|---|---|
| [자료구조] 트리 - 탐색 트리 (0) | 2022.12.20 |
| [자료구조][파이썬으로 쉽게 풀어쓴 자료구조] 05 큐 문제풀기 (0) | 2022.10.25 |
| [자료구조] 큐 - 우선순위 큐를 활용한 미로 탐색 (0) | 2022.10.25 |
| [자료구조] 큐 - BFS 미로 탐색 (0) | 2022.10.25 |